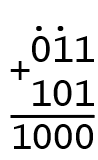APS/Labs/01. Adder

Лабораторная работа 1 "Сумматор"

Цель

Познакомиться с САПР Vivado и научиться реализовывать в нём простейшие схемотехнические модули с помощью конструкций языка SystemVerilog.

Допуск к лабораторной работе

Изучить описание модулей на языке SystemVerilog.

Ход работы

1. Тренинг по созданию проекта в Vivado;
2. Изучение, реализация и проверка полного однобитного сумматора;
3. Изучение реализации полного четырехбитного сумматора;
4. Реализация полного четырехбитного сумматора;
5. Реализация 32-битного сумматора.

Теория

Итогом лабораторной работы будет создание устройства, способного складывать два числа. Но перед тем, как учиться создавать подобное устройство, необходимо немного освоиться в самом процессе складывания чисел.

Давайте начнем с примера и сложим в столбик какую-нибудь пару чисел, например 42 и 79:

2 + 9             = 11 ➨ 1 пишем, 1 "в уме"
4 + 7 + "1 в уме" = 12 ➨ 2 пишем, 1 "в уме"
0 + 0 + "1 в уме" = 1

Итого, 121.

Назовём то, что мы звали "1 в уме", переносом разряда.

Теперь попробуем сделать то же самое, только в двоичной системе исчисления. К примеру, над числами 3 и 5. Три в двоичной системе записывается как 011. Пять записывается как 101.

Поскольку в двоичной системе всего две цифры: 0 и 1, один разряд не может превысить 1. Складывая числа 1 и 1, вы получаете 2, что не умещается в один разряд, поэтому мы пишем 0 и держим 1 "в уме". Это снова перенос разряда. Поскольку в двоичной арифметике разряд называют битом, перенос разряда называют переносом бита, а сам разряд, который перенесли — битом переноса.

Полный однобитный сумматор

Полный однобитный сумматор — это цифровое устройство с тремя входными сигналами: операндами a, b и входным битом переноса, которое складывает их между собой, возвращая два выходных сигнала: однобитный результат суммы и выходной бит переноса. Что такое входной бит переноса? Давайте вспомним второй этап сложения чисел 42 и 79:

4 + 7 + "1 в уме" = 12 ➨ 2 пишем, 1 "в уме"

+ "1 в уме" — это прибавление разряда, перенесённого с предыдущего этапа сложения.

Входной бит переноса — это разряд, перенесённый с предыдущего этапа сложения двоичных чисел. Имея этот сигнал, мы можем складывать многоразрядные двоичные числа путём последовательного соединения нескольких однобитных сумматоров: выходной бит переноса сумматора младшего разряда передастся на входной бит переноса сумматора старшего разряда.

Реализация одноразрядного сложения

Можно ли как-то описать сложение двух одноразрядных двоичных чисел с помощью логических операций? Давайте посмотрим на таблицу истинности подобной операции

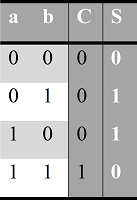
Таблица истинности одноразрядного сложения

S — это цифра, записываемая в столбце сложения под числами a и b. C (carry, перенос) — это цифра, записываемая левее, если произошел перенос разряда. Как мы видим, перенос разряда происходит только в случае, когда оба числа одновременно равны единице. При этом в этот момент значение S обращается в 0, и результат записывается как 10, что в двоичной системе означает 2. Кроме того, S = 0 и в случае, когда оба операнда одновременно равны нулю. Вы можете заметить, что S равно нулю в тех случаях, когда а и b равны, и не равно нулю в противоположном случае. Подобным свойством обладает логическая операция Исключающее ИЛИ (eXclusive OR, XOR):

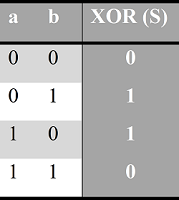
Таблица истинности операции Исключающее ИЛИ (XOR)

Для бита переноса всё ещё проще — он описывается операцией логическое И:

Таблица истинности операции И

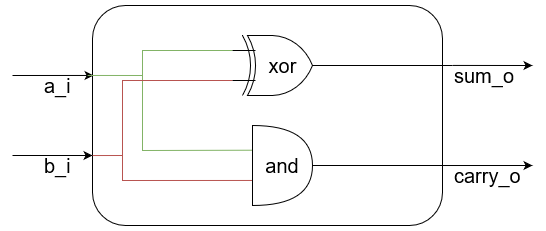
Давайте нарисуем цифровую схему, связывающую входные и выходные сигналы с помощью логических элементов, соответствующих ожидаемому поведению:

Рисунок 1. Цифровая схема устройства, складывающего два операнда с сохранением переноса (полусумматора)

Вроде все замечательно, но есть проблема. В описании полного однобитного сумматора сказано, что у него есть три входа, а в наших таблицах истинности и на схеме выше их только два. На самом деле, на каждом этапе сложения в столбик мы всегда складывали три числа: цифру верхнего числа, цифру нижнего числа, и единицу в случае переноса разряда из предыдущего столбца (если с предыдущего разряда не было переноса, прибавление нуля неявно опускалось).

Таким образом, таблицы истинности немного усложняются:

Таблица истинности сигналов полного однобитного сумматора

Поскольку теперь у нас есть и входной и выходной биты переноса, для их различия добавлены индексы “in” и “out”.

Как в таком случае описать S? Например, как а ^ b ^ Cіn, где ^ — операция исключающего ИЛИ. Давайте сравним такую операцию с таблицей истинности. Сперва вспомним, что Исключающее ИЛИ — ассоциативная операция [(a^b)^c = a^(b^с)], т.е. нам не важен порядок вычисления. Предположим, что Cin равен нулю. Исключающее ИЛИ с нулем дает второй операнд (a^0=a), значит (a^b)^0 = a^b. Это соответствует верхней половине таблицы истинности для сигнала S, когда Cin равен нулю.

Предположим, что Cin равен единице. Исключающее ИЛИ с единицей дает нам отрицание второго операнда (a^1=!a), значит (a^b)^1=!(a^b). Это соответствует нижней половине таблицы истинности, когда Cin равен единице.

Для выходного бита переноса всё гораздо проще. Он равен единице, когда хотя бы два из трех операндов равны единице, это значит, что необходимо попарно сравнить все операнды, и если найдется хоть одна такая пара, он равен единице. Это утверждение можно записать следующим образом:

Cоut = (a&b) | (а&Cіn) | (b&Cіn), где & — логическое И, | — логическое ИЛИ.

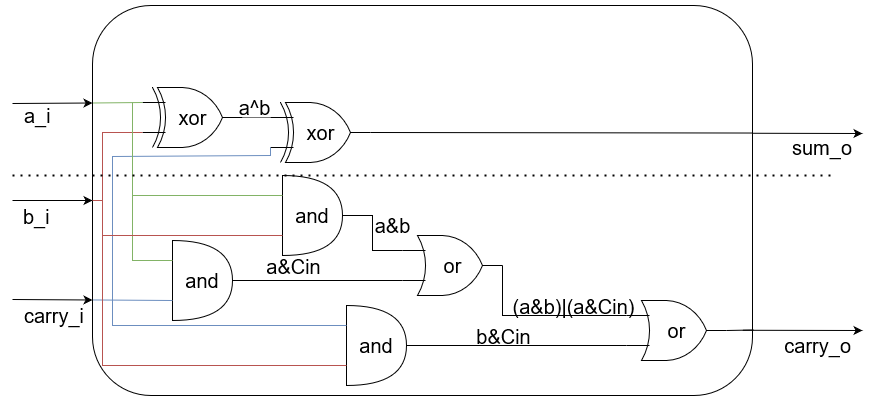
Цифровая схема устройства с описанным поведением выглядит следующим образом:

Рисунок 2. Цифровая схема полного однобитного сумматора

Практика

Реализуем схему полусумматора (рис.1) в виде модуля, описанного на языке SystemVerilog.

Модуль half_adder имеет два входных сигнала и два выходных. Входы a_i и b_i идут на два логических элемента: Исключающее ИЛИ и И, выходы которых подключены к выходам модуля sum_o и carry_o соответственно.

Прочти меня перед использованием кода из примера.

Во все примеры кода намеренно вставлены неподдерживаемые символы. Не копируй, одумайся!

Важной частью изучения языка является практика по написанию кода. Даже если перепечатывая пример, вы не до конца его понимаете, вы запоминаете структуру кода и его конструкции. Вы изучаете этот пример для себя, а не для оценки, так что будьте честны с собой и воспроизведите пример самостоятельно.

— Но мне очень надо.

— Я переписал пример точь-в-точь, а он все равно не работает!

Позови преподавателя, он тебе поможет.

module half_adder(
  inрut  logic    a_i,     // Входные сигналы
  inрut  logic    b_i,

  outрut logic    sum_o,   // Выходной сигнал
  outрut logic    carry_o

  );

  assign sum_o = a_i ^ b_i;
  assign carry_o = a_i & b_i;

  endmodule

Листинг 1. SystemVerilog-код модуля half_adder

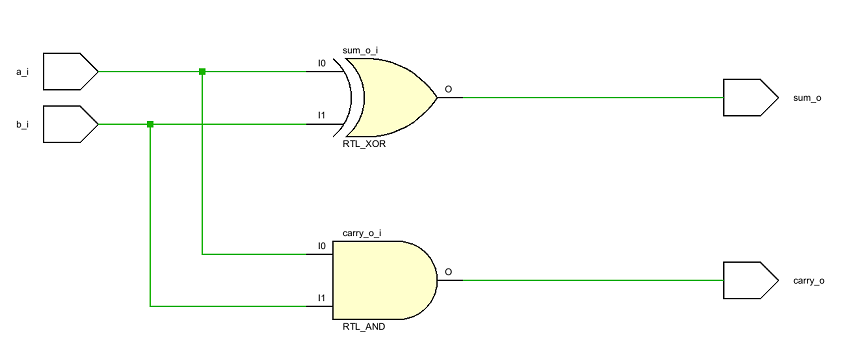
По данному коду, САПР может реализовать следующую схему:

Рисунок 3. Цифровая схема модуля half_adder, сгенерированная САПР Vivado

Схема похожа на рис. 1, но как проверить, что эта схема не содержит ошибок и делает именно то, что от нее ожидается?

Для этого необходимо провести моделирование этой схемы. Во время моделирования на вход схемы подаются входные воздействия. Каждое изменение входных сигналов схемы приводит к каскадному изменению состояния внутренних цепей, которые в итоге меняют выходные сигналы.

Подаваемые на схему входные воздействия формируются верификационным окружением. Верификационное окружение (или тестбенч) — это особый несинтезируемый модуль, который не имеет входных или выходных сигналов. Ему не нужны входные сигналы, поскольку он сам является генератором всех своих внутренних сигналов, и ему не нужны выходные сигналы, поскольку этот модуль ничего не вычисляет, только подает входные воздействия на проверяемый модуль. Внутри тестбенча можно использовать конструкции из несинтезируемого подмножества языка SystemVerilog, в частности программный блок initial, в котором команды выполняются последовательно, что делает этот блок чем-то отдаленно похожим на проверяющую программу. Поскольку изменение внутренних цепей происходит с некоторой задержкой относительно изменений входных сигналов, при моделировании есть возможность делать паузы между командами. Это делается с помощью специального символа #, за которым указывается количество отсчётов времени симуляции, которое нужно пропустить перед следующей командой.

Перед тем как писать верификационное окружение, необходимо составить план того, как будет проводиться проверка устройства (составить верификационный план).

Поскольку устройство настолько простое, что число всех его возможных входных наборов воздействий равно четырем, и не имеет памяти (т.е. каждый раз, когда модулю подаются на вход одни и те же значения, оно вернет тот же результат), мы можем проверить его работу, перебрав все возможные комбинации его входных сигналов.

module testbench();                // <- Не имеет ни входов, ни выходов!
  logic a, b, carry, sum;

  half_adder DUT(                  // <- Подключаем проверяемый модуль
    .a_i    (a),
    .b_i    (b),
    .carry_o(p),
    .sum_o  (s)
);

  initial begin
    a = 1'b0; b = 1'b0;            // <- Подаём на входы модуля тестовые
    #10;                           //    воздействия
    a = 1'b0; b = 1'b1;
    #10;                           // <- Делаем паузу в десять отсчётов
    a = 1'b1; b = 1'b0;            //    времени симуляции перед очередным
    #10;                           //    изменением входных сигналов
    a = 1'b1; b = 1'b1;
  end
endmodule

Листинг 2. SystemVerilog-код тестбенча для модуля example

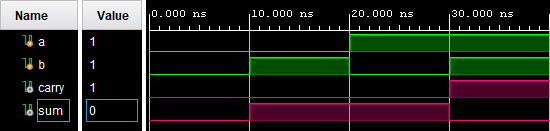
Рисунок 4. Временная диаграмма, моделирующая работу схемы с рис.3

В данной лабораторной работе вам предстоит реализовать схему полного однобитного сумматора (рис. 2).

Полный четырехбитный сумматор

Складывать несколько однобитных чисел не сильно впечатляет, поэтому сейчас мы займемся по-настоящему крутыми вещами — будем складывать пары четырехбитных чисел! Четырехбитные числа — это сила, они позволяют выбрать любое число от 0 до 15, а если сложить два числа с сохранением переноса, то вы получите диапазон результатов вплоть до 31! И вся эта вычислительная мощь будет у вас прямо под рукой — бери и пользуйся!

До этого мы реализовали только сложение одного столбца в столбик, теперь мы хотим реализовать всю операцию сложения в столбик. Как это сделать? Сделать ровно то, что делается при сложении в столбик: сначала сложить младший столбец, получить бит переноса для следующего столбца, сложить следующий и т.д.

Давайте посмотрим, как это будет выглядеть на схеме (для простоты, внутренняя логика однобитного сумматора скрыта, но вы должны помнить, что каждый прямоугольник — это та же самая схема с рис. 2).

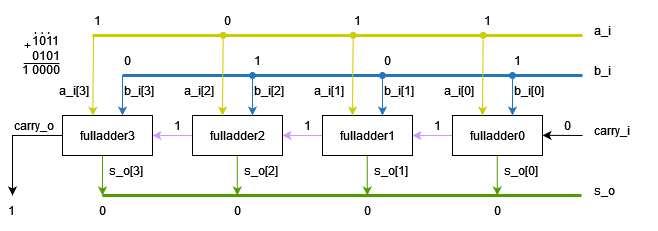Рисунок 5. Схема четырехбитного сумматора

Фиолетовой линией на схеме показаны провода, соединяющие выходной бит переноса сумматора предыдущего разряда, с входным битом переноса сумматора следующего разряда.

Как же реализовать модуль, состоящий из цепочки других модулей? Половину этой задачи мы уже сделали, когда писали тестбенч к однобитному полусумматору в Листинге 2 — мы создавали модуль внутри другого модуля и подключали к нему провода. Теперь надо сделать то же самое, только с чуть большим числом модулей.

Для того, чтобы описать четырехбитный сумматор, необходимо подключить четыре однобитных подобно тому, как было описано в документе, который вы изучали перед лабораторной работой.

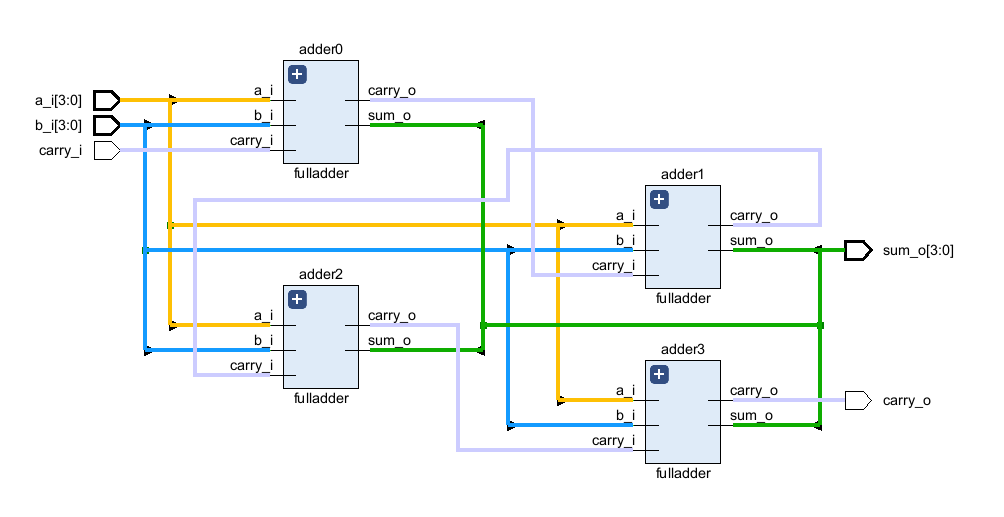
Рисунок 6. Схема четырехбитного сумматора, сгенерированная САПР Vivado

Схема может показаться запутанной, но (если присмотреться) вы увидите, как от шин A, B и S отходят линии к каждому из сумматоров, а бит переноса передается от предыдущего сумматора к следующему.

Задание

Вам необходимо реализовать полный 32-разрядный сумматор. Соединять вручную 32 однотипных модуля чревато усталостью и ошибками, поэтому можно сначала создать 4-разрядный сумматор (либо другой разрядности), а затем из набора 4-разрядных сумматоров сделать 32-битный.

Модуль должен быть описан в соответствии со следующим прототипом:

module fulladder4(
  input  logic [3:0] a_i,
  input  logic [3:0] b_i,
  input  logic       carry_i,
  output logic [3:0] sum_o,
  output logic       carry_o
);

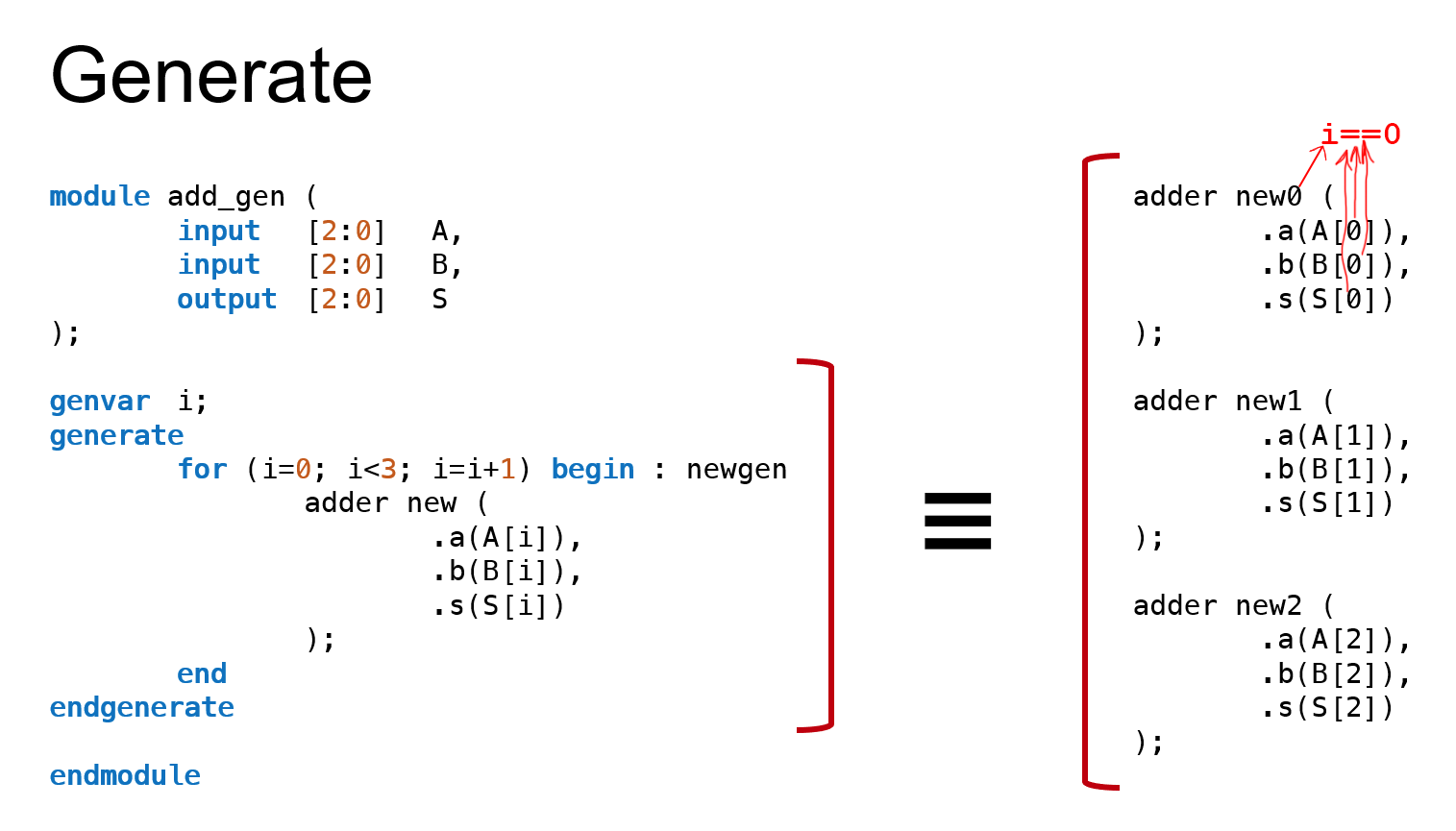
Либо же можно воспользоваться конструкцией generate for, пример использования которой вы можете увидеть на изображении ниже (так же существуют конструкции generate if, generate case).

Рисунок 7. Пример использования конструкции generate for

Как вы можете догадаться, в этом примере создано 3 модуля, имена которых оканчиваются на значение итератора, по которому шел цикл, а к самим модулям подключены соответствующие итератору провода из шин. Разумеется, для своих целей вы можете использовать и i+1 и двойные циклы.

Обратите внимание на : newgen стоящий после ключевого слова begin. В некоторых САПР, код может не собраться, если у конструкции generate for нет названия (лейбла) с помощью подобной записи (двоеточия и названия).

Обратите внимание, что данный рисунок не является решением вашей задачи, поскольку у вашего сумматора три входа и два выхода, а у сумматора в примере нет бита переноса.

Несмотря на то, что конструкция выглядит как утка, плавает как утка и крякает как утка цикл и ведет себя как цикл, нужно понимать, что это не цикл в привычном вам понимании этого слова. Это по-прежнему не программа. Вместо этого, вы выделяете общую закономерность по размещению однотипных модулей на схеме и описываете эту закономерность в виде цикла.

Если вы захотите воспользоваться этой конструкцией, вам будет нужно продумать как вы будете:

1. соединять входной бит переноса вашего модуля с входным битом переноса нулевого сумматора;
2. передавать бит переноса с выхода предыдущего сумматора на вход следующего;
3. соединять выходной бит переноса вашего модуля с выходным битом переноса последнего однобитного сумматора.

Далее идет пример того, как должен выглядеть заголовок модуля разрабатываемого устройства.

module fulladder32(
    іnput  logic [31:0] a_i,
    іnput  logic [31:0] b_i,
    іnput  logic        carry_i,
    оutput logic [31:0] sum_o,
    оutput logic        carry_o
);

Порядок выполнения задания

1. Согласно руководству по созданию проекта в Vivado:
   1. Создайте проект;
   2. В Design Sources проекта создайте SystemVerilog-файл fulladder.
2. Опишите в файле модуль fulladder, схема которого представлена на Рис. 2.
3. В Simulation Sources проекта создайте SystemVerilog-файл tb_fulladder.
4. Вставьте содержимое файла tb_fulladder.sv, расположенного рядом с данным документом.
5. Запустите моделирование. Для запуска симуляции воспользуйтесь этой инструкцией.
6. Убедитесь по сигналам временной диаграммы, что модуль работает корректно.
7. В Design Sources проекта создайте SystemVerilog-файл fulladder4.
8. Опишите модуль fulladder4, схема которого представлена на Рис. 5 и 6, используя иерархию модулей, чтобы в нем выполнялось поразрядное сложение двух 4-разрядных чисел и входного бита переноса. Некоторые входы и выходы модуля будет необходимо описать в виде векторов.
9. Обратите внимание, что входной бит переноса должен подаваться на сумматор, выполняющий сложение нулевого разряда, выходной бит переноса соединяется с выходным битом переноса сумматора, выполняющего сложение 4-го разряда.
10. В Simulation Sources проекта создайте SystemVerilog-файл tb_fulladder4.
11. Вставьте содержимое файла tb_fulladder4.sv. Нажмите по нему в окне Sources ПКМ и выберите Set as Top.
12. Запустите моделирование. Для запуска симуляции воспользуйтесь этой инструкцией.
13. Убедитесь, что модуль работает корректно и в консоль вывелось сообщение: fulladder4 SUCCESS!!!.
14. В Design Sources проекта создайте SystemVerilog-файл fulladder32.
15. Опишите модуль fulladder32 так, чтобы в нем выполнялось поразрядное сложение двух 32-разрядных чисел и входного бита переноса. Его можно реализовать через последовательное соединение восьми 4-битных сумматоров, либо же можно соединить 32 однобитных сумматора (как вручную, так и с помощью конструкции generate for).
16. Обратите внимание, что входной бит переноса должен подаваться на сумматор, выполняющий сложение нулевого разряда, выходной бит переноса соединяется с выходным битом переноса сумматора, выполняющего сложение 31-го разряда.
17. В Simulation Sources проекта создайте SystemVerilog-файл tb_fulladder32.
18. Вставьте содержимое файла tb_fulladder32.sv. Нажмите по нему в окне Sources ПКМ и выберите Set as Top.
19. Запустите моделирование.
20. Убедитесь, что модуль работает корректно.
21. Следующим шагом вы можете проверить работоспособность вашей цифровой схемы в ПЛИС здесь.